Задачи для подготовки к контрольной работе по теме "Соотношения между сторонами и углами прямоугольного треугольника" можно скачать здесь.

Некоторые задачи для подготовки к контрольной работе:

1. В прямоугольной трапеции меньшее основание равно 3см, большая боковая сторона равна 4см, а один из углов равен 150⁰. Найти площадь трапеции.
2. Катеты прямоугольного треугольника равны 9 дм и 40 дм. Найдите гипотенузу и площадь треугольника.
3. В равностороннем треугольнике АВС высота CH равна 5V3. Найдите стороны этого треугольника и его площадь. (5V3 - пять корней из трех)
4. В прямоугольном треугольнике АВС DА = 90⁰, АВ = 20см, высота AD = 12см. Найти АС и cos C.
5. В треугольнике АВС угол С равен 90°, угол А равен 60°, ВС=50V3 (пятьдесят корней из трех). Найдите АВ.
6. Высота BD прямоугольного треугольника АВС равна 24см и отсекает от гипотенузы АС отрезок DC, равный 18см.  Найти АВ и cos А.
7. В прямоугольном треугольнике АВС  угол С - прямой, АВ = 8 см, угол АВС равен 45 градусов.  Найдите: а)  АС;    б) высоту CD, проведенную к гипотенузе.
8. В прямоугольном треугольнике ОМН гипотенуза МН равна 10 см. Найдите катет ОМ, если косинус угла М равен 0,6.
9. Найдите острые углы прямоугольного треугольника, если его катеты равны 3 см и 3V3 см (три корня из трех).

 

Теория:
 

1. Пропорциональные отрезки. Отношение отрезков.
2. Определение подобных треугольников. Коэффициент подобия.
3. Свойство биссектрисы треугольника.
4. Отношение площадей подобных треугольников.
5. Признаки подобия треугольников.
6. Средняя линия треугольника. Определение.
7. Теорема о средней линии треугольника.
8. Свойство медиан треугольника.
9. Свойство высоты прямоугольного треугольника, проведенной из вершины прямого угла.
10. Утверждения о пропорциональных отрезках в прямоугольном треугольнике...
11. Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
12. Значения синуса, косинуса и тангенса для углов 30º, 45º и 60º.​
13. Как определить на местности высоту предмета и расстояние до недоступной точки.
14. Подобие произвольных фигур. Коэффициент подобия.
15. Центрально-подобные фигуры.

 

Задачи  к зачету и контрольной по теме "Подобные треугольники"

1. Рис.1 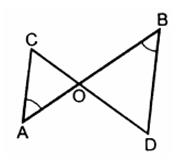  Углы А и В равны, СО=4, DО=6, АО=5. (Рис.1). Найдите: а) ОВ; б) отношение АС к BD; в) отношение площадей треугольников АОС и BOD. 
2. В треугольнике АВС АВ=4 см, ВС=7 см, АС=6 см, а в треугольнике МNK МК=8 см, MN=12 см, KN=14 см. Найдите углы треугольника MNK, если угол А равен 80 градусов, угол В равен 60 градусов.
3.  Рис.2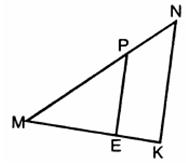Отрезок РЕ параллелен NK, МР=8, MN=12, ME=6. (Рис.2) Найдите: а)  МК; б) отношение РЕ к NK; в) отношение площадей треугольников МЕР и MKN.
4. Рис.3 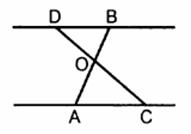      Дано: АО=6,8 см; СО=8,4 см; ОВ=5,1 см; OD=6,3 см. (Рис.3). Докажите, что  прямая АС параллельна прямой BD. Найдите: а) отношение DB к AC; б) отношение периметров треугольников АОС и DBO: в) отношение площадей треугольников DВО и АОС. 
5. Диагонали ромба ABCD пересекаются в точке О, BD=16 см. На стороне АВ взята точка К так, что ОК перпендикулярен АВ и ОК = 4см. Найдите сторону ромба и вторую диагональ.
6.  Рис.4 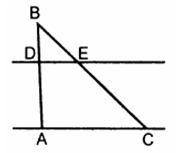 Дано: D=3,1 см; ВЕ=4,2 см; ВА=9,3 см, ВС=12,6 см. (Рис.4). Докажите, что прямая DE параллельна прямой AC. Найдите: а) отношение DE к AC; б) отношение периметров треугольников АBС и DBE; в) отношение площадей треугольников DВE и АBС.
7. Прямая пересекает стороны треугольника АВС в точках М и К соответственно так, что МК параллельна АС, ВМ : АМ=1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см.
8. В выпуклом четырехугольнике ABCD АВ=9 см, ВС=8 см, CD=16 см. AD=6 см, BD=12 см. Докажите, что ABCD – трапеция.
9. В трапеции ABCD (AD и ВС основания) диагонали пересекаются в точке О, AD=12 см, ВС=4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см².
10. В равнобедренном треугольнике MNK с основанием МК=10 см, MN=NK=20см. На стороне NK лежит точка А так, что AK : AN= 1 : 3. Найдите АМ.

 

Задачи для подготовки к контрольной работе и зачету по теме "Подобные треугольники" можно   скачать здесь  и тут:  (скачать) 

Вопросы к зачету по теме "Подобные треугольники"
 

План-конспект доказательства признаков подобия треугольников.