Сайт учителя
Понятие квадратного уравнения
ax²+bx+c=0, где a, b, c - некоторые числа, причем a≠0, а x - корень уравнения
называется квадратным уравнением.
Квадратное уравнение называется ещё уравнением второй степени, так как левая часть уравнения - многочлен второй степени.
Коэффициенты уравнения:
a – старший коэффициент (коэффициент при x²),
b – второй коэффициент (коэффициент при x),
с – свободный член.
D – дискриминант квадратного трехчлена, находящегося в левой части уравнения, короче - дискриминант квадратного уравнения.
D=b²-4ac
Если дискриминант квадратного трехчлена положительное число, то этот трехчлен можно разложить на множители:
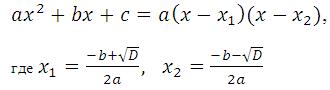
Множители (x-x1) и (x-x2) называются линейными множителями.
Если x=x1 или x=x2, то выполняется равенство квадратного трехчлена нулю, значит числа x1 и x2 являются корнями квадратного уравнения.
Если хотя бы один из коэффициентов квадратного уравнения (кроме коэффициента при х²) равен нулю, то квадратное уравнение называют неполным.