Квадратное уравнение называется неполным, когда хотя бы один из коэффициентов уравнения равен нулю.

Напомним, что коэффициент при x² не может быть равен нулю. В этом случае уравнение будет не квадратным, а линейным.

Итак, если хотя бы один из коэффициентов (кроме а)  равен нулю, то квадратное уравнение принимает один из трех видов:

1)   Пусть b≠0, с=0,  тогда уравнение примет вид  ax²+bx=0.

Решим его способом разложения на линейные множители:

Вывод: если в квадратном уравнении  с=0,  b≠0,  то один из  его корней обязательно равен нулю.

2)   Пусть b=0, с≠0, тогда уравнение примет вид  ax²+c=0.

Решим его способом разложения на линейные множители:  

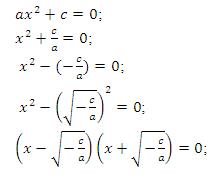
Обратим отдельное внимание на число под знаком корня. Напомним, что знак минус не означает, что это число отрицательное. Он показывает, что это число противоположное.

Поэтому если коэффициенты а и с – числа одного знака, то уравнение не будет иметь корней, так как под знаком квадратного корня окажется отрицательное число.  Если коэффициенты а и с - числа разных знаков, то уравнение будет иметь два корня, отличающиеся только знаками.

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю (а другой при этом не теряет смысла). Поэтому решим отдельно два линейных уравнения, являющиеся множителями в нашем квадратном уравнении:

3)      Если   b=0   и   с=0, то уравнение принимает вид  ax²=0.

Корнем этого уравнения является только число ноль.